利用者:Testscreenings/Ivy port/OriginalAlgo

back Ivy port

original algorithm

defenitions and so forth

- Ivy

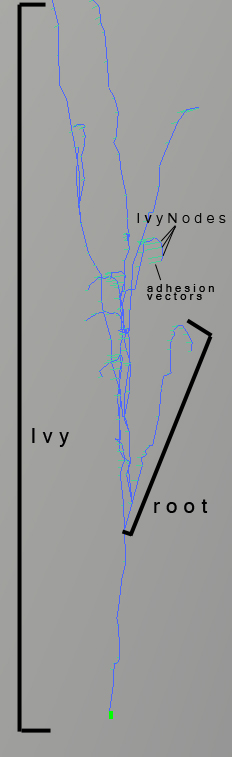
- IvyNode

- IvyRoot

Data Structure

All the data of the Ivy is stored in three Node-classes. Here are short descriptions as well as a first translation into Python.

- IvyNode

   This is the most basic Nodetype.
   It stores the position and other attributes of one point on one root of the Ivy.

class IvyNode():
    def __init__(self, climbing, length, floatingLength):
        self.climbing = False
        self.length = 0.0
        self.floatingLength = 0.0
    
    # node position
    position = (0,0,0)
    
    # primary grow direction, a weighted sum of the previous directions
    primaryVector = (0,0,0)
    
    #adhesion vector as a result from other scene objects
    adhesionVector = (0,0,0)
    
    # a smoothed adhesion vector computed and used during the birth phase,
	#  since the ivy leaves are align by the adhesion vector, this smoothed vector
	#  allows for smooth transitions of leaf alignment
    smootAdhesionVector = (0,0,0)
    
    # length of the associated ivy branch at this node
    length = 0.0
    
    # length at the last node that was climbing
    floatingLength = 0.0
    
    # climbing state
    climbing = False

- IvyRoot

   This Node is basically a container for one Root of the Ivy
   and stores all the containing IvyNodes,
   as well as its living state

class IvyRoot():
    # List with containing IvyNodes
    ivyNodes = []
    
    # living state of this Root
    alive = True
    
    # number of parents, represents the level in the root hierarchy
    parents = 0

- Ivy

   Ivy is the base Node.
   It stores the IvyRootNodes.

class Ivy():
    # list of containing Roots
    ivyRoots = []
    
    # the ivy size factor, influences the grow behaviour [0..0,1]
    ivySize = 1.0
    
    # leaf size factor [0..0,1]
    leafSize = 1.0
    
    # branch size factor [0..0,1]
    branchSize = 1.0
    
    # maximum length of an ivy branch segment that is freely floating [0..1]
    maxFloatingLength = 1.0
    
    # maximum distance for adhesion of scene object [0..1]
    maxAdhesionDistance = 1
    
    # weight for the primary grow vector [0..1]
    primaryWeight = 0.5
    
    # weight for the random influence vector [0..1]
    randomWeight = 0.5
    
    # weight for the gravity vector [0..1]
    gravityWeight = 0.5
    
    # weight for the adhesion vector [0..1]
    adhesionWeight = 0.5
    
    # the probability of producing a new ivy root per iteration [0..1]
    branchingProbability = 0.5
    
    # the probability of creating a new ivy leaf [0..1]
    leafingProbability = 0.5
    
    # in the C++ version the functions for seeding, growing, birthing, etc
    # are also placed inside this class.
    # I show them here, but it is probably better to place them somewhere else eventually
    # Or maybe I don't really understand how the C++ class is working and how these really fit in here.
    # I am deffing them here, but i really am not sure if that is what the C++ Code does.
    
    # resetting
    def resetSettings():
        pass
        
    # initialize a new ivy root
    def seed():
        pass
        
    # one single grow iteration
    def grow():
        pass
        
    # compute the adhesion of scene objects at a point pos
    def computeAdhesion():
        pass
        
    # computes the collision detection for an ivy segment
    # oldPos->newPos, newPos will be modified if necessary
    def computeAdhesion():
        pass
        
    # creates the ivy triangle mesh
    def birth():
        pass

growing algorithm

This is a short description of the original algorithm of the ivy generator.

The main part of the algorithm lies in the grow function. From the initial seed point new Ivynodes are spawned and placed.

the position of the new Nodes is determined in three steps.

- the first step is to generate a new position depending on several variables.

   - (A)a primary Vector
   - (B)a random Vector
   - (C)an adhesion vector
   
       -these variables are normalized in respect to each other and individually weighed
       according to user input
       - growVector = (A * Aweight) + (B * Bweight) + (C * Cweight)
   
   - (D)a gravity Vector
       - gravityVector = ((0,0,-1)) * localIvySize * gravityWeight
       - gravityVector *= pow((previousNode.floatingLength / local_maxFloatLength), 0.7f)
       - the gravityVector acts then on the new Node with userweighting
       and depending on the floatinglength of the current ivysegment
       
   -the above result then in the new position of the next node:
       new_pos = previousNode.position + growVector + gravityVector

- now the new position is checked against the colliding Mesh

   - test if the root collides
       - test if the root should die
       - change the new_pos so it doesn't intersect with the mesh anymore
       - set it's climbingState according to collisionState
       
   - if the new_pos was changed: update the growVector according to the new_pos
       - growVector = newPos - previousNode.position - gravityVector

- in the third step a new IvyNode is generated and its settings are set

   - newNode.position = new_pos
   - newNode.primaryVector = ( 0.5 * previousNode.primaryVector +
                               0.5 * growVector.normalize() )
   - newNode.adhesionVector = adhesionVector
   - newNode.length = previousNode.length +
                      (new_pos - previousNode.position).length()
   - newNode.floatingLength = length of conected floating IvyNodes
   - newNode.climbing = climbing (from the collision detection)
   
   

- the last step here is now to put this newNode in the list of IvyNodes of the corresponding IvyRootNode

helper functions / algorithms

compute adhesion

this are my preliminary notes on adhesion:

   ok, first: what does he exactly want to do here?
   the function returns the adhesionVector. so my best guess would be that
   this is the force and direction towards the surface.
   combined with the adhesionWeight this then defines how strongly the Ivy wants to stick to the surface.
   
   so how does he do that?:
   -check for nearest face of the mesh
   -now this again i don't quiet get:
       -scalar product projection of old_pos to the center of the fface?:
           float nq = Vector3d::dotProduct(t->norm, pos - t->v0->pos)
   -check if the projection nq(?) is on the outer side of the face
       if not: continue
   
  -...
  
  -compute barycentric coordinates of p0  <<<?>>>
  
  -at last compute normalized direction of adhesion
  -and multiply it with the distance to the surface divided by the scale_factor of the local_maxAdhesion
  -return the adhesionVector
  
  ####### obviously the middle i haven't figured out yet #########

compute collision

this are my notes so far on the collision detection. they are neither complete nor are they correct to the point of certainty.

   basic steps:
       thought: maybe implement and octree for the faces
                to efficiently discard the one too far away?
   
       ### http://www.flipcode.com/archives/Basic_Collision_Detection.shtml
       
       
   - test if old_pos --> new_pos is passing through the hyperplane of the polygon
                                               not sure about this one (below)
       direction = new_pos.dot(face.normal) + (old_pos - face.center).length
       if direction > 0:
           new_pos_placement = 'plane_front'
       else:
           new_pos_placement = 'plane_back'
       return new_pos_placement
       
   - test if the path old_pos --> new_pos passes through the boundaries of the polygon
       --> find the intersectionpoint():
       ray_vector = (old_pos - new_pos).normalize()
       t = -(face.normal.dot(old_pos) + (old_pos - face.center).length) /
           face.normal.dot(ray_vector)
           ### check if face.normal.dot(ray_vector) is zero: if yes: do something ###
       intersectPoint = old_pos + ray_vector * t
       return intersectPoint
       
       --> test if intersectPoint is on the polygon():
           ### An Efficient Ray-Polygon Intersection
           ### by Didier Badouel from Graphics Gems I :
           ### http://graphics.stanford.edu/courses/cs348b-98/gg/intersect.html
   
   ###################################################
   if you have read all of the above: nice
   actuall i remembered we have this whole rayintersection test
   as a function of objects. much simpler.
   obj.ray_cast(old_pos, new_pos)
   returns [hitlocation, hitnormal at face, faceindex]
   
   ####################################################
   now: what do i think does the original function do:
   it tests if the new_pos is intersecting some part of the mesh (doh)
   if yes it adjusts the new_pos as to move it out of the mesh again
   it also sets the climbingState of the RootNode:
       if it intersects the climbing is set to true
       if not climbing is set to false
       not sure about the following:
           the climbing is important for the adhesion i think
           the longer the chain of non climbing RootNodes
               --> something should be done i think (?)
               - suggestions? (maybe look elsewhere better :) )