利用者:Pepribal/Notas/Topología

Las mallas están formadas por vértices, aristas y caras. Una arista conecta dos vértices. Las caras están formadas por 3 o más aristas. Las caras están definidas por el número de aristas (o vértices) que contienen. Una cara con 3 aristas (o vértices) es un triángulo. Una con 4 vértices es un quad. Con más aristas, es un N-gon. Las caras son renderizables, ya que representan una superficie, mientras que los vértices y aristas no lo son. Las aristas siempre son rectas. Todos los vértices de una cara concreta deberían ser coplanares, o casi coplanares. En el caso de los triángulos esto siempre se cumple. En el caso de los quads, es relativamente sencillo que sean casi coplanares. Con los N-gons, hay que ser muy cuidadoso, ya que solo sirven para definir porciones planas de la superficie; para superficies curvas, lo más adecuado son los triángulos y los quads. Sin embargo, los quads son mucho más deseables, ya que los triángulos pueden ocasionar problemas al animar y al subdividir. Así, solo son aceptables los triángulos cuando la malla no vaya a ser subdividida ni animada.

Edge loops (bucles de aristas)

Los bucles de aristas (y de caras) se usan en modelado orgánico, especialmente cuando la forma de la malla debe ser animada (deformada) de un modo no lineal.

Edge loops: 4 bucles de borde que terminan en las esquinas (A), bucle de borde a hueco (B), de hueco a hueco (C y F), bucle de hueco (D), de borde a borde (E), bucle cíclico (G), de polo a polo (H) y de hueco a polo (I)

Un edge loop es un conjunto de aristas conectadas que sigue la arista central en cada cruce de 4 caminos (4-way junction). Un 4-way junction es un vértice conectado a 4 aristas. Si seguimos una arista hasta un vértice de esas características, encontraremos 3 posibilidades (aristas) para continuar el trayecto: la que está en el medio es la que debemos tomar para seguir con el edge loop adecuado.

Un vértice conectado a un número de aristas distinto de 4 se denomina un polo. Un cruce de 3 caminos es un polo N (N-pole), mientras que un cruce de 5 caminos es un E-pole. Una malla bien construida no tiene polos de más de 5 aristas.

Los edge loops pueden ser cíclicos o terminar en:

• un polo,
• un hueco, o
• un borde.

Puede considerarse un borde como un hueco infinito.

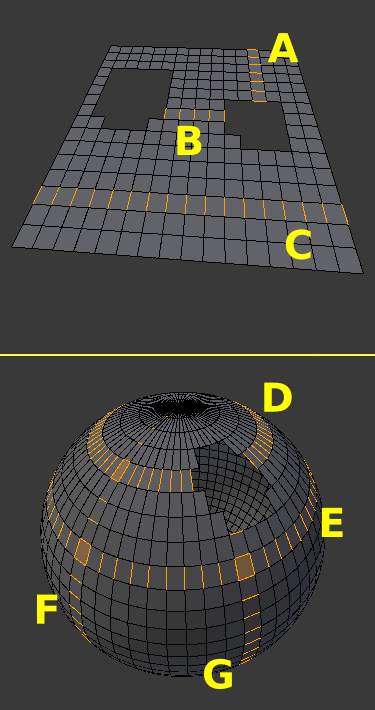
Blender reconoce como edge loops, además, conjuntos de aristas que delimitan bordes o huecos:

Los bucles de aristas tienen sentido cuando hablamos de caras de 4 aristas, y, en menor grado, de 3 aristas. Independientemente del comportamiento de Blender, nos bucles de aristas carecen de sentido cuando involucramos N-gons.

Los bucles son esenciales en superficies animadas que se deforman (encogen, doblan, estiran,...). Ello se aplica al modelado orgánico y la animación, principalmente. Los bucles se deberían colocar siguiendo las líneas de deformación de la malla, o de lo contrario pueden producirse desagradables tensiones visibles en la superficie. En el caso de seres animados, significa que los bucles deberían seguir los músculos deformadores. Hay mucha teoría acerca de cómo modelar, usar edge loops, gestionar polos, etc. para construir models animados adecuadamente. Sin embargo esto queda más allá del alcance de este artículo.

Para seleccionar edge loops, usaremos 3D View » Select » Edge Loop en modo edición, en modo de selección de vértice o arista, y todos los bucles de aristas a los que pertenezcan las aristas seleccionadas serán seleccionados. También puede usarse AltRMB o ⇧ ShiftAltRMB para seleccionar el edge loop al que pertenece la arista sobre la que hacemos clic. Esta herramienta precisa que las aristas estén conectadas a caras; de lo contrario, lo que obtendremos será la selección de toda la geometría de alambre conectada.

Edge rings (anillos de aristas)

Edge rings: de borde a hueco (A), de hueco a hueco (B y D), de borde a borde (C), anillo cíclico (E), de triángulo a triángulo (F) y de hueco a triángulo (G)

Un anillo de aristas es un conjunto de aristas no conectadas que siguen un "camino" definido por las aristas opuestas de cada quad. Son las aristas que unen dos edge loops paralelos y consecutivos.

Los anillos de aristas pueden ser cíclicos o terminar en:

• un hueco,
• un borde, o
• una cara distinta a un quad (triángulo o N-gon).

Todas las aristas del anillo perteneces a 2 quads, excepto las terminales, que pueden pertenecer a un solo quad o ser compartidas por un quad y una cara no quad.

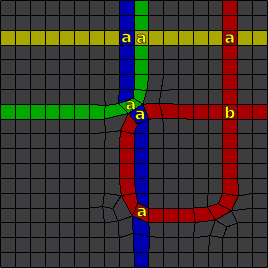
Normalmente 2 anillos de aristas fluyen a lo largo de cada quad: uno en la dirección de dos aristas opuestas, y otro en la dirección de los otros dos. Puede suceder que el mismo anillo de aristas fluya dos veces a través de un quad (anillo de aristas con auto-intersección). En la figura pueden verse ejemplos de anillos que intersectan: en anillo E intersecta con el G y F; el anillo F intersecta también con el anillo D. Obsérvese que las 4 aristas quedan seleccionadas en los quads de la intersección.

Para seleccionar anillos de aristas automáticamente, se utiliza 3D View » Select » Edge Ring en modo edición, en modo de selección de vértices o aristas, y todos los anillos de aristas a los que pertenezcan las aristas seleccionadas serán seleccionados. Puede usarse también CtrlAltRMB o ⇧ ShiftCtrlAltRMB para seleccionar el anillo de aristas al que pertenece la arista sobre la que hacemos clic.

Face loops (bucles de caras)

Face loops: algunos bucles de caras resaltados con distintos colores; los quads en los que intersectan están marcados (a), y en los que auto-intersectan están marcados (b)

Un bucle de caras está compuesto por todos los quads (y solo quads) que contribuyen con aristas en un edge ring. Cada anillo de aristas tiene una relación directa con un bucle de caras, y viceversa.

Normalmente, hay 2 face loops fluyendo a través de cada quad: uno en la dirección de dos aristas opuestas, y el otro en la dirección de las otras 2. Sin embargo puede suceder que el mismo face loop pase dos veces por el mismo quad (bucle de caras con auto-intersección), una en cada dirección.

Para seleccionar face loops, se puede usar CtrlAltRMB o ⇧ ShiftCtrlAltRMB en modo edición, en modo de selección de caras, para seleccionar el face loop al que pertenece la cara sobre la que aplicamos la acción. El bucle de caras seleccionado será el que fluya en la dirección de la arista más cercana al punto donde hagamos clic.

Geometría manifold y no manifold

La geometría no manifold es una geometría irreal. Hay que tener en cuenta que las caras de las mallas tienen grosor 0, por lo que una malla con bordes (huecos infinitos) o huecos (bordes interiores) es irreal. Una malla manifold es una malla cuyas aristas (y vértices) son todos manifold. Intuitivamente, una superficie manifold define completamente (envuelve) un volumen cerrado, sin intersecciones consigo misma, y no tiene agujeros abiertos o bordes. La geometría no manifold es inconsistente y se considera mala topología: algunas operaciones no se pueden realizar en mallas no manifold, debido a que no se puede determinar qué lado de la superficie es 'dentro' y qué lado es 'fuera'.

Para seleccionar toda la geometría no manifold de un objeto malla, se utiliza 3D View » Select » Non Manifold (⇧ ShiftCtrlAltM) en modo edición, en modo de selección de vértices o aristas.

Hay varios tipos de geometría no manifold. Si echamos un vistazo al panel redo, después de ejecutar la anterior acción, a parte de definir si queremos ampliar la selección o no, podemos elegir qué tipo de geometria no manifold queremos seleccionar:

• Wire: todas las aristas que no pertenecen a ninguna cara.
• Boundaries: aristas de borde, incluyendo agujeros (huecos).
• Multiple Faces: aristas que pertenecen a 3 o más caras.
• Non Contiguous: aristas que perteneciendo a 2 caras, estas tienen normales opuestas.
• Vertices: vértices que pertenecen a aristas wire; vértices que pertenecen a aristas multiple faces; vértices aislados; vértices que son el único medio de unión entre caras (geometría con anchura 0).

Topology mirror (reflexión de topología)

Al editar mallas, existe la opción de editar un lado de la misma, de tal modo que el otro lado sigue las acciones realizadas. Ello se puede conseguir marcando X Mirror (panel Mesh Options en la barra lateral Tool Shelf). Lo que hace esta herramienta es reflejar todas las acciones de cada vértice en su correspondiente vértice simétrico del otro lado de la malla.

El vértice correspondiente es el que es perfectamente simétrico del que se está modificando. La simetría se calcula a lo largo del eje local X, es decir, el plano local YZ actúa como espejo. Los vértices que no tienen vértice correspondiente simétrico en el punto exacto al otro lado del espejo no producirán una acción reflejada en el otro lado.

Sin embargo, si el reflejo está activado, tenemos una opción adicional: si marcamos Topology Mirror, la correspondencia de pares de vértices se calcula de una forma distinta. En lugar de utilizar la posición espacial de los vértices, se tiene en cuenta la posición topológica.

La posición topológica de un vértice se calcula usando un número de identificación único (UID) basado en la cantidad de vértices vecinos (conectados al vértice actual a través de una arista), y en los UID de esos vecinos, que a su vez tendrán en consideración los UID de sus vecinos, siguiendo ello recursivamente hasta que toda la malla se haya tomado en consideración. Si los vértices fueran casas y las aristas calles, el UID de un vértice sería comparable a la dirección postal exacta de la casa.

Si una malla no tiene simetría topológica, entonces todos sus vértices tienen UIDs únicos. Sin embargo, si la malla es perfectamente simétrica topológicamente, entonces cada vértice compartirá el mismo UID con el vértice correspondiente en el otro lado. Ello es, ambos vértices tendrán la misma dirección postal (en cada lado).En ese caso, cuando un vértice es movido y el reflajado de topología está activo, el vértice correspondiente recibirá las acciones reflejadas a lo largo del eje local X (a través del plano local YZ).

Sin embargo, si el vértice tiene más de una correspondencia, entonces no se ejecuta esta acción de simetría topológica. Es el caso de mallas con múltiples simetrías, o con formas muy simples, como el cubo, la esfera UV, o un grid. Para que ello funcionara, habría que eliminar todas las simetrías excepto una.