利用者:Pepribal/Ref/Appendices/Warp
The Warp tool
This tool is available in object mode and edit mode. In the first, it acts on the selected objects centers: it modifies the location coordinates without affecting the rotation or scale properties of the object. In edit mode, it acts on selected vertices. Explanation will be made for objects, but it also applies to vertices in the very same manner.
The warp tool (⇧ ShiftW), found in 3D View » Object » Transform » Warp in object mode, and 3D View » Mesh » Transform » Warp in edit mode, rotates the selected objects centers or vertices around the viewport Z axis with origin at the 3D cursor.
The final rotation applied will depend on each object particular position on the viewport, the viewport orientation, the location of the 3D cursor and the amount of effect given to the tool (Angle value). Angle can be defined, initially, moving the mouse to the left and to the right, interactively. After the operation is confirmed (with the usual way for interactive operations), it can be tweaked from the Warp panel.
Intuitively, it can be seen that the initial vertical position of each object, relative to the 3D cursor, will define its radius of rotation around it. On the other hand, the initial horizontal position (relative to 3D cursor as well) will determine how much the object will be affected by the Angle value. The further from the 3D cursor (horizontally), the bigger the effect. Objects to the right of the 3D cursor will rotate counterclockwise for positive values of Angle; objects to the left, will rotate inversely; objects just above or below it will not rotate at all.
However, how does the algorithm behave specifically?
Maths behind the warp tool
This section is for the mathematician or the curious. It doesn't have really useful information for artists.
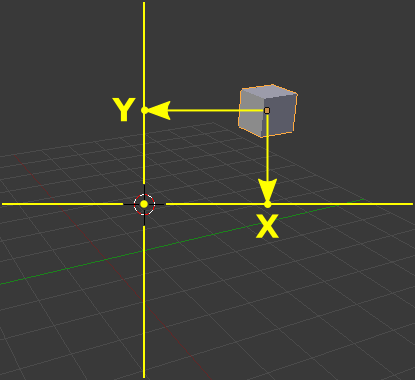
So, consider we have the following set of objects {<math>O_1</math>, <math>O_2</math>,..., <math>O_n</math>}, which are the selected objects over which the warp operation will be performed. The viewport coordinates of each object <math>O_i</math> is the 2D vector (<math>X_i</math>, <math>Y_i</math>), as shown in Object coordinates for the Warp tool.
The radius of rotation of each object <math>O_i</math> will be given by its viewport Y (vertical) coordinate relative to the 3D cursor (<math>Y_i</math>).
A value of 0.0 of Angle will just project each object into the viewport YZ plane, along the viewport X direction: that is the starting point for every one of the selected objects.
Let's consider the set of horizontal (X) coordinates of all the selected objects: {<math>X_1</math>, <math>X_2</math>,..., <math>X_n</math>}. These values represent the respective original distance of each one of the objects to the viewport YZ plane (centered at the 3D cursor). Now, we are interested in the horizontal coordinates of the leftmost and rightmost objects (in the viewport XY plane), which we will call, respectively, <math>X_L</math> and <math>X_R</math>.
The distance (<math>D</math>) between these two extreme objects is defined as:
<math>D = X_R - X_L</math>
When all selected objects are aligned vertically on the viewport, or when there is only one selected object, it happens that <math>D</math> equals 0.0. In those cases, for the following calculations, the former formula will be replaced by the following one:
<math>D = 0.1</math>
Let's define now <math>A_i</math> as the value of Angle which causes the object <math>O_i</math> to rotate 360° counterclockwise (positive angle). This value turns out to be:
<math>A_i = \frac{360 \times D}{X_i}</math>
In the particular case in which <math>X_i</math> has zero value, the value <math>A_i</math> would be infinite, meaning that the object <math>O_i</math> doesn't rotate at all.
The effect of Angle can be better understood if we take into consideration the following: if Angle has a value of <math>V</math>, then a given object <math>O_i</math> (with horizontal coordinate <math>X_i</math>) will be rotated <math>R</math> degrees as depicted by this formula:
<math>R = V \times \frac{X_i}{D}</math>
From this, we can see the following:
- The final rotation <math>R</math> will have the same sign than the value of Angle if <math>X_i</math> is positive, or the opposite sign if it is negative (<math>D</math> is always positive).
- A zero value of Angle will always produce a zero rotation.
- The bigger the absolute value of <math>X_i</math>, the bigger the final rotation for a particular object; moreover, if <math>X_i</math> is zero, there will be no rotation.
Remember that a positive angle rotation is counterclockwise.