利用者:RedTriangle/Bevel

Bevel

Inputs:

• a set of selected vertices and edges of the model.
• the value of the indent, in which we want to build a bevel.
• the number of segments for interpolation of bevels shape.

Goals:

It is necessary to build a bevel along the selected edges. Bevel can have different shapes (straight line or round).

The algorithm of construction of bevel:

1. The analysis of the input vertices

To construct a bevel it is necessary to determine how to connect new polygons with each other. For this purpose we should analyze the input vertices.

Support points are calculated for each selected vertex. Each vertex can comprise random number of selected and not selected edges . Support points are calculated using the following rules:

• Support point can be located on adjacent edges with the selected edges.
• Support point can be located between the selected edges.

Position of the point is determined by the size of the indent. The point between the edges on the sum of the vectors between vectors formed by selected edges. For each selected vertex we fill following data structures.

/* list of new vertices formed around v */
typedef struct AdditionalVert{
        struct AdditionalVert *next, *prev;
        BMVert *v;                      /* parrent vertex */
        ListBase vertices;              /* List of auxiliary vertices */
        int count;                      /* count input edges, alse count additioanl vertex */
        int countSelect;                /* count input selection edges */
} AdditionalVert;

Each support vertex is stored in the following structure

/* Item in the list of additional vertices */
typedef struct VertexItem{
	struct VertexItem *next, *prev;
	BMVert *v;
	int onEdge;		/*	1 if new vertex located on edge; edge1 = edge, edge2 = NULL
				*	0 if new vert located betwen edge1 and edge2
				*	3 additional vert for rounding case	*/
	BMEdge *edge1;
	BMEdge *edge2;
	BMFace *f;
	float hv[3];	        /* coordinate of support vertex */
	AdditionalVert *parent;
} VertexItem;

2. Construction of new polygons

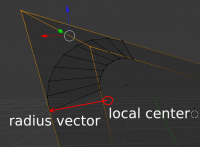
New polygons will be located along selected edges. Each vertex of the selected edge is associated with support points which have been found in step 1. Only adjacent points are determined. A new polygon is based on these points. For the case of a round bevel it is necessary to build a round shape along the selected edge. For this purpose perpendiculars to the edges are defined , center of the inscribed circle is calculated.

Round shape is obtained by rotating of the radius-vector around the axis directed along of the selected edge. The points located on the adjacent unselected edges are calculated as an intersection of generatrices with the plane defined through three support points which have been found in step 1.

3. Generation of polygons around vertices

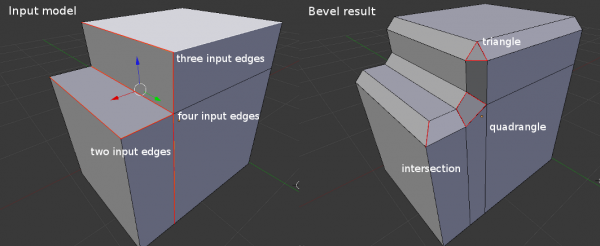
After the construction of new polygons along the edges, we need to build new polygons around vertexes . There are two main cases:

• If the vertex includes two edges, then the surface around the point is formed as intersection of new polygons.
• If the vertex includes more than two edges, then we need to build around this vertex N-gon formed by additional points.

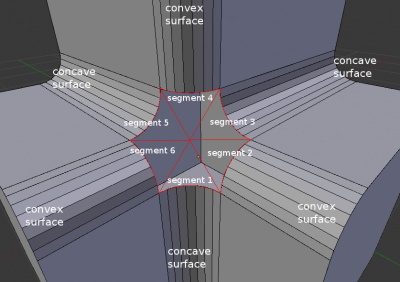
3.1 Construction of smooth surfaces

In the case of a round bevel it is necessary to construct a smooth surface rather than a simple N-gon. This is a difficult task. It is necessary to consider the set of particularities. For example the vertex may include edges with different shapes of smoothing - some of them may be convex, other ones - concave. To take into account such cases, I propose to build this surface by segments. For each segment is filled a data structure that contains the shape parameters and boundary vertices.

typedef struct SurfaceEdgeData {
        BMEdge *e;
        BMVert *a, *b;                                  
        BMVert *boundaryA, *boundaryB;  
        // список текущих точек
        ListBase vertexList;
        int count;
        float h[3];                                             
} SurfaceEdgeData;

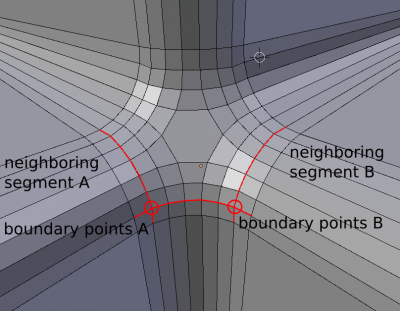
Construction of polygons round profile segment. In this case, of particular importance are the points located on the border segments.For calculate the boundary points we should to find the adjacent segments. In the three segments (current and two adjacent), calculated as the round profiles (as in step 2). The boundary points are the nearest points between by appropriate profiles.

When structures of each segment will be filled, new points can be calculated, and polygons can be constructed. If the parameter of segmentation is an odd number, the last segment will be the N-gon, formed by boundary points of the segments.

4. Rebuilding of existing polygons

The geometry of all the adjacent polygons will be changed as a result of building bevel. A set of related polygons and additional points that are connected with the polygon is defined for each of the selected edge. The points that are not selected, is stayed unchanged. Support points is used instead of selected points. The new polygon is built on these points. The old polygon is deleted.

5. Removing of selected items

After all of constructions are made we can delete the selected input vertices and edges.

Links

http://www.youtube.com/watch?feature=player_embedded&v=HuHzcHQIJoY#!

http://www.youtube.com/watch?feature=player_embedded&v=q3LBWfLNopE

Examples