利用者:Apinzonf/Gsoc2014/design
目次
Design
Project: Interactive Quadrilateral Remeshing Based on Harmonic Functions.
Language: C, C++.
This new tool goes:
- (First option) into the specials menu, because the tool do not working in real time.
- (Second option) special session like sculpt or knife session.
- (Third option) Modifier like laplacian deform tool.
Introduction
This document describes the steps to achieve the quadrilateral remeshing in an interactive way.
Background
This project use the methodology proposes by Dong et al. Named “Harmonic functions for quadrilateral remeshing of arbitrary manifolds”.
Methodology
The project is composed by the following steps:
- Build an initial scalar field
This scalar field assigns a value to each vertex, this set will describe generally as the remeshing was performed.
This scalar field uses several weights assigned in some special vertices how constraints. These special vertices are for example the peak of the head, or arms.
These weights have extreme minimum and maximum values, and the algorithm interpolate a scalar field between all special vertices.
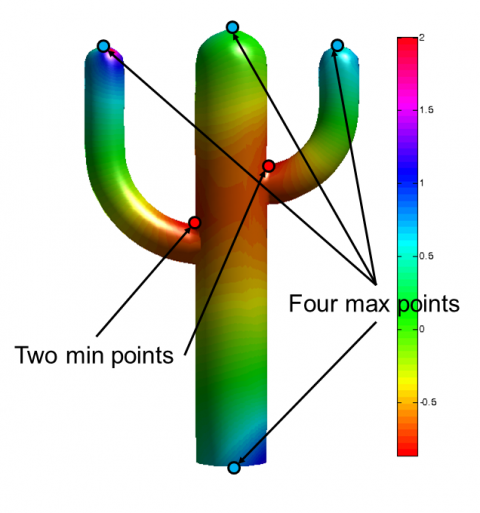
In the figure (Initial scalar field), show an example of the initial scalar field computed for 6 feature points (Two min points with weight -1, four max points with weight 1). The color represents the value computed for every vertex in the mesh. - Based on harmonic scalar field compute a gradient field.
From scalar field U derive two orthogonal piecewise-constant tangent vector fields G1, G2 - Form a net of polygons over the surface by tracing integral lines of the vector fields G1 and G2.
- Eliminate all T-junctions and triangulate polygons with more than 4 vertices.
Deliverables
Midterm
- Interactive session with user to define features points.
- Construct the harmonic scalar field.
- Based on harmonic scalar field compute a gradient field.
- Define two orthogonal vector fields using the gradient field.
Final
- Define a net of polygons over the original surfaces with the use of integral lines defined by the orthogonal vector fields.
- Generate a new mesh.