利用者:Jjoonathan/Trim Algorithms (Update)

Boolean AND, Boolean SUB against grid

It is critical that the trimming code be able to handle subsequent overlapping boolean operations. Before, the operations were assumed to happen all at once, which simplified the code at the expense of generality: you could trim as many polygons as you wanted so long as they never overlapped. I expected this approach to work (punched holes don't often overlap) until I found trims in my sample files constructed from overlapping trim triangles, so I had to implement the fully general mechanism for the sake of compatibility.

The previously written code discovered its intersections entirely based on information provided by the raster algorithm (line-grid intersection). In order to handle intersections between a line and and an arbitrary polygon that no longer necessarily represented a rectangular cell, I wrote new code that looped through all cells touched by the line and within each cell looped through all descendants of the original chopped polygon looking for intersections. This also required rewriting the code that propagated interior/exterior state along polygon edges since that code was not adapted to the case where the underlying mesh structure was not a grid.

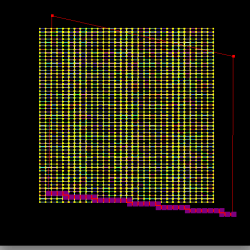
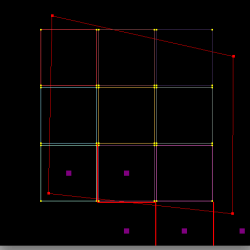
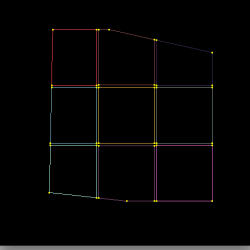
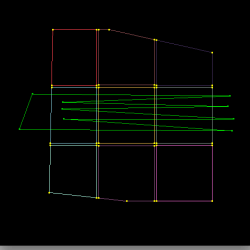
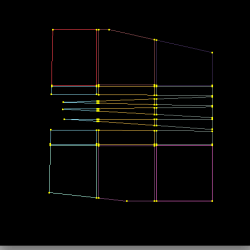
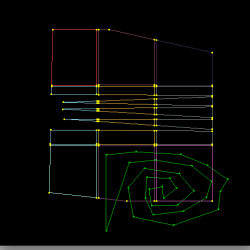
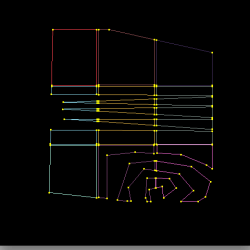
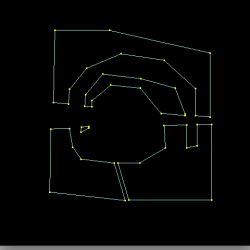
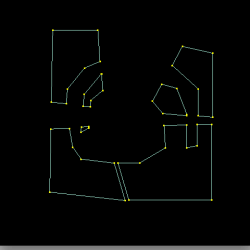
The red trimming polygon represents the AND operation (typically used to define the exterior of a patch) while the green trimming polygons represent the SUB operation (used to cut holes). The magenta squares and thick red lines represent the output of the raster algorithm (visited cells, edges respectively). This algorithm is used to reduce the cost of trimming from O(M*N*N) (for a trim poly of M sides and a N*N mesh) to O(M).

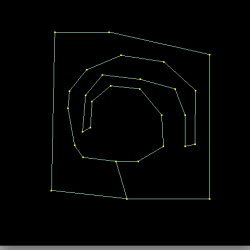
Cuts made within a single polygon are another edge case that needs special handling. In order to use the BLI_polyfill tessellator (which uses the ear-clipping strategy and is not tolerant towards explicit holes). The main challenge is discovering a pair of suitable vertices between which to connect the interior and exterior polygons. This task is performed by choosing a semi-random first-guess and iterating by replacing endpoints of the connecting line by endpoints of any corresponding intersections. This leads to a satisfactory result even in geometrically challenging situations (e.g. a spiral within a spiral). If the internal and external polygons have the same orientation (sign of area) then one of them must be flipped so that the combined inner/outer polygon winds correctly.

Integration of Trimming in Blender

The second task I worked on last week was bringing this code out of the GLUT demonstration app and into blender proper. Tasks that are done:

• BRep surfaces are read from imported files and decoded into multiple surfaces in a single curve.

• Surfaces carry along an attached pointer to exterior (Bool AND) and interior (Bool SUB) trim curves.

• Data structures of the meshgrid have been altered so that they coincide with the format expected from polyfill and display list construction.

Tasks that are left to do:

• Write code to translate trim curves into the "Nurb" structure format

• Make a control for the user-specificed subdivision resolution of these curves

• Evaluate the trim curves at the specified number of points, call GridMesh's boolean operations, and then call polyfill from within the displaylist construction routine