利用者:Apinzonf/laplacian/test solvers

Performance Testing of Solvers

In this document we present the performance evaluation of some numerical solvers for our Laplacian Smooth system.

I need to solve the following system of equations.

Difusion equation for mesh smoothing:

<math>\frac{\partial V}{\partial t}=\lambda L\left( V\right) </math>

Integrating the diffusion equation with a explicit Euler scheme:

<math>\left( I+\lambda dtL\right) V^{t+1}=V^{t}</math>

Where <math>V^{t}</math> is the actual position of vertex, and <math>V^{t+1}</math> is the vertex after smoothing.

Solving the sparse linear system

<math>Ax=b</math>

Where:

<math>A=\left( I+\lambda dtL\right) </math>

<math>x=V^{t+1}</math>

<math>b=V^{t}</math>

Setup

Hardware Specification

• Processor: AMD Quad-Core 2.40 GHz

• RAM: 8.0 GB

• OS: Windows 7 Professional

• Graphics controller: NVIDIA Quadro FX 570

Software Specification

• CGAL Computational Geometry Algorithms Library

• Graphite Research platform for computer graphics

Numeric Solvers Used

• CG: Conjugate gradient method.

• BICGSTAB: Biconjugate gradient stabilized method.

• GMRES: Generalized minimal residual method.

• SUPERLU: Sparse Direct Solver, LU decomposition with partial pivoting.

• TAUCS_LLT: A library of sparse linear solvers with LLT factorization.

• TAUCS_LU: A library of sparse linear solvers with LU decomposition.

• TAUCS_LDLT: A library of sparse linear solvers with LDLT factorization.

• CHOLMOD: Supernodal sparse Cholesky factorization.

• FASTCG: Fast Conjugate gradient.

• ARPACK: Solver for symmetric matrices.

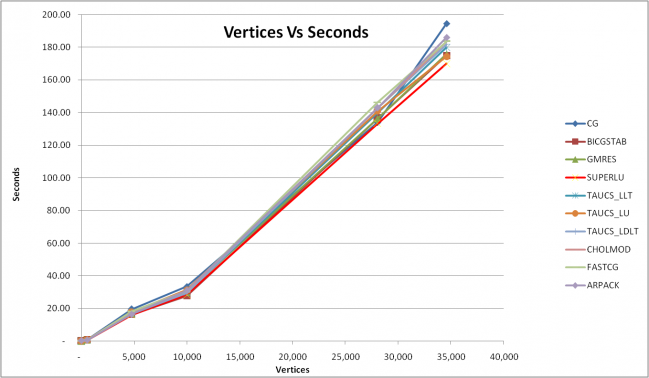
Results

Numerical solver SuperLU is faster than the other methods.

The difference between the solvers is not representative.

Model	Vertices	Edges	Faces	CG	BICGSTAB	GMRES	SUPERLU	TAUCS_LLT	TAUCS_LU	TAUCS_LDLT	CHOLMOD	FASTCG	ARPACK
cruz	24	44	22	0.05	0.05	0.04	0.04	0.05	0.04	0.05	0.05	0.05	0.50
Motionblender31	538	1608	1072	0.83	0.63	0.71	0.61	0.69	0.63	0.68	0.79	0.62	0.63
Ymodel	4770	14304	9536	19.60	16.44	16.93	16.06	16.65	17.61	16.88	17.95	18.23	16.56
mesh_0120	10002	30000	20000	33.43	27.76	29.91	28.54	29.72	31.43	29.53	30.80	30.51	30.97
neptune	28052	84168	56112	133.97	136.46	136.39	133.21	139.98	140.79	142.87	142.76	146.22	142.96
Armadillo	34594	103776	69184	194.48	174.88	175.80	169.92	179.88	174.37	181.70	183.49	183.56	185.99

Vertices Vs Seconds