利用者:Jjoonathan/New NURBS Eval

New NURBS Evaluation Code

The NURBS evaluation code is the code that transforms the curve's mesh from a flat, trimmed 2D representation into a surface that follows the control points. Blender's old NURBS evaluation code had two significant drawbacks: it did not compute surface partial derivatives and it did not allow for robust handling of discontinuities. This wasn't a problem before trimming because without trimming the edge cases produced by approximating normals directly from the mesh were quite manageable. Unfortunately, the (literal) edge cases multiply uncontrollably down for trimmed surfaces, so a more sophisticated evaluation code must be used. Additionally, higher derivatives are algorithmically useful (e.g. calculating tessellation resolution to satisfy an error bound) and the new evaluation code ought to be faster (1/2 to 1/4th as many divisions).

Verification Against Mathematica NURBS Implementation

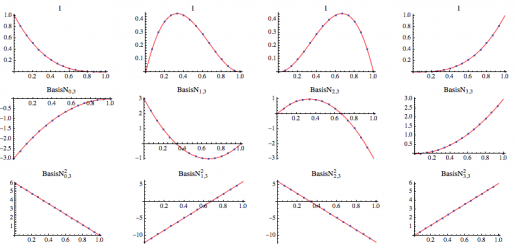The new code to evaluate BSpline basis functions can now handle edge cases (approach a knot from left vs right without a seam-inducing fudge factor). It also calculates derivatives and handles the case of arbitrarily many coinciding internal knots correctly.

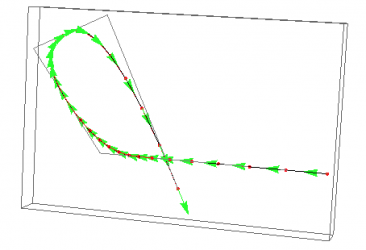
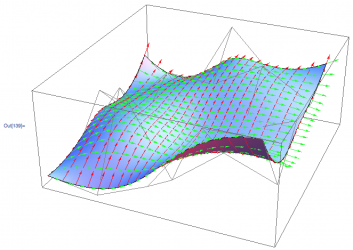
Here you can see the new BSpline and BSpline derivative evaluation code (dots, arrows respectively) compared to Mathematica's internal BSpline evaluation code (black line, blue surface) for verification purposes.

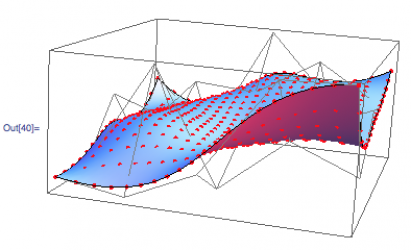
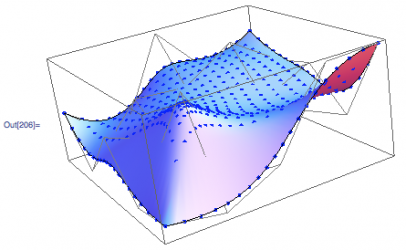
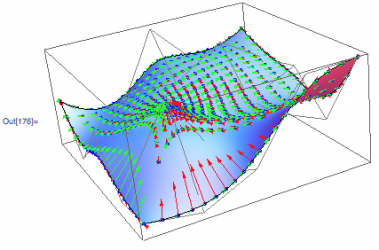
Here you can see the new NURBS and NURBS derivative evaluation code (dots, arrows respectively) compared to Mathematica's internal NURBS evaluation code (black line, blue surface) for verification purposes. The difference between NURBS and BSpline becomes important in the evaluator: NURBS surfaces have weights for each control point while BSplines do not. The weights significantly increase the difficulty of computing derivatives.

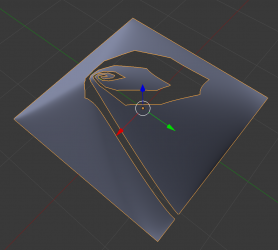
Here you can see the effect that having good normals has on the appearance of surfaces. Compare to normals calculated automatically from the mesh.

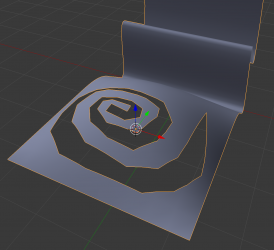
Rhino does not represent cyclic surfaces using cyclic NURBS bases. Instead, it simply connects the endpoints of a NURBS sheet. This used to create a problem for blender because it would calculate normals based on a polygon corner, creating a very obvious discontinuity at the seam. Now the seam is invisible, as it should be.

Analytical partial derivative evaluation works for nonrational (weighted) surfaces too!

Features that need to be implemented before .3dm import works

1. I must finish the import code for trim curves. Note that the spiral you see above was not imported. It's a hardcoded test curve to make sure the trim-enabled tessellator is functioning.

2. Rotation surfaces

Hopefully by next week! *crosses fingers