利用者:Mats Halldin/Sandbox/Incubator-003
Introduction to topology.
目次
[非表示]Euler's theorem
- Euler's theorem
- Let P be a polyhedron which satisfies:
- (a) Any two vertices of P can be connected by a chain of edges (i.e. there are no faces missing and no "Non-Manifolds".)
- (b) Any loop on P which is made up of straight line segments separates P into two pieces (i.e. a mesh without holes like in a donut.)
- Then <math>v-e+f=2</math> for P.
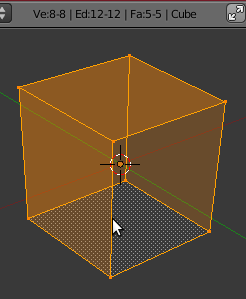
Default cube
If we add a cube and tab into edit mode, all vertices are select by default and above the 3D view Blender is informing us that
Ve:8-8 | Ed:12-12 | Fa:6-6 | Cube
which, of course, means we have selected all eight vertices, twelve edges, and six faces of our object Cube.
According to Euler's theorem
- <math>v-e+f=2</math>
if we take the number of vertices (v), subtract the number of edges (e), and add the number of faces (f)
- <math>8-12+6</math>
we get 2.
If we extrude a face from our cube, Euler still returns
- <math>12-20+10=2</math>.
And if we hit CtrlT to transform all quads into tris, Euler still returns
- <math>12-30+20=2</math>.
On the other hand, if we remove a single face from our original cube, Euler returns
- <math>8-12+5=1</math>
instead.
Other simple primitives
Let's test Euler's theorem on other well-known geometric primitives:
Now, add a default UV Sphere and tab into edit mode. Blender now informs us that
Ve:482-482 | Ed:992-992 | Fa:512-512 | Sphere
and Euler returns
- <math>482-992+512=2</math>.
Extruding (<math>486-1000+516=2</math>) or deleting (<math>482-992+511=1</math>) a face from the UV sphere is not changing the output from Euler's formula.
Same goes for the default cylinder
Ve:576-576 | Ed:1152-1152 | Fa:576-576 | Cylinder- <math>66-160+96=2</math>.
We might first hope that this is a golden rule that applies unconditionally to all meshes.
Some more complex cases
The default torus
Ve:576-576 | Ed:1152-1152 | Fa:576-576 | Torus- <math>576-1152+576=0</math>.
A monkey
Cubes, spheres, and even toruses are well-known geometrical shapes, but what about Suzanne, our monkey? In edit mode, Blender tell us
Ve:507-507 | Ed:1005-1005 | Fa:500-500 | Monkey
and Euler returns
- <math>507-1005+500=2</math>.
Looks familiar. However, if we deselect everything and Ctrl⇧ Shift⇆ TabM to select Non-Manifolds, Blender selects two pairs of loops, namely the holes for the eyes. Apparently, the monkey is topologically distinct from the default cube.
Furthermore, if we CtrlT on the monkey and select all tris, we get
- <math>507-1472+968=3</math>.
Selecting non-manifolds again returns an additional edge near the nose.
Uh-huh, topology-wise something is wrong here.
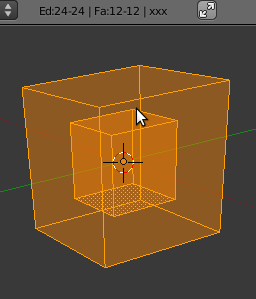
Cube with interior cube
Select all vertices of the default cube, ⇧ ShiftD to duplicate, and S to scale it down. Our mesh now has two cube, one inside the other. Blender tells us
Ve:16-16 | Ed:24-24 | Fa:12-12 | Cube
and Euler returns
- <math>16-24+12=4</math>.
This is new...
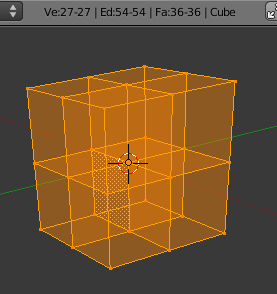
Cube with interior faces
- <math>27-54+36=9</math>
Möbius strip and Klein bottle
A Möbius strip
- <math>32-48+16=0</math>
A Klein bottle is what you get if you glue two Möbius strips together along a common edge.
- <math>624-1248+624=0</math>
Odd as they come, these two meshes are, according to Euler's theorem, similar to a circle...
Conclusions
Is there any logic to this?
- Circle=0
- Disc=1
- Cylinder=2
- If two polygons meet they do so in a common edge, and each edge of a polygon lies in precisely one other polygon.
- At any vertex, faces fit together to form a piece of surface around that vertex.
- Is there a loop that does not separate the mesh into two distinct parts?
References
- Armstrong, M. A. (1983), Basic Topology, Springer, pp 1–12, ISBN 0387-90839-0.