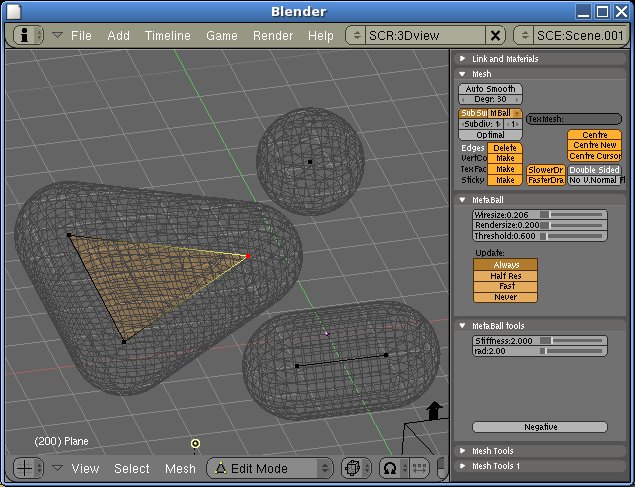
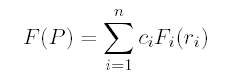Dev:Source/Modeling/MetaMesh
目次
[非表示]MetaMesh
MetaMesh project is part of my thesis. Purpose of this project is to create simple and easy way of MetaBall editting. Non-manifold Mesh will be directing structure for MetaBalls.
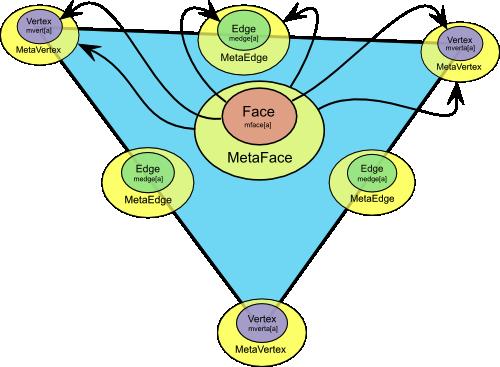
Data structure
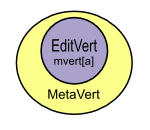
- visualisation of MetaVert data structure:
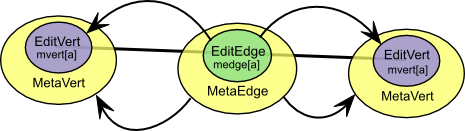
- visualisation of MetaEdge data structure:
- visualisation of MetaFace data strucure:
Theory of MetaBalls
Implicit Function
Polygonised surface of MetaBalls is just set of points in space with the same value of implicit function:
where F(P) is value of implicit funciton. Points at polygonised surface has zero value. c parameter is "stiffness" of each MetaElem. F blending function and r is distance from each MetaElem.
Blending Function
We use Blending function with this form:
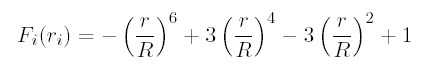
|
r parameter is distance from MetaElem and R is radius of MetaElem. MetaElem behind this radius has no influence at polygonised surface.
Computation of distance from directing structures
Point (Vertex)
Distance from point is very easy to computate:
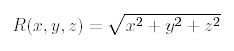
|
Segment (Edge)
Computation of distance from segment isn't so easy as computation distance from a point. I will show you how hard it is if we computate it 3D space. I don't do it so stupid, of course ;-)
Segment is part of the line. Line is identified by two points A[a0, a1, a2], B[b0, b1, b2] in space. Parametric simultaneous sequations of line has these form:
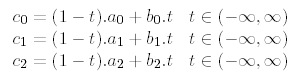
|
At the first time we have to computate parameter tI of rectangular projection of point P[p0, p1, p2] to the line.
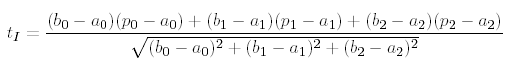
|
If parameter tI is inbetween <0,1> then we can computate position C[c0, c1, c2] of this projection using previous simultaneous equations. If parameter tI is bigger then 1 or smaller then 0 value, then it means, then rectangular projection doesn't intersects segment.
If rectangular projection intersects segment then distance from this segment is:
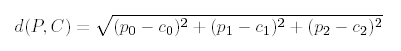
|
It rectangular projection doesn't intersect segment, then we have to computate distance from point P[p0, p1, p2] to the both end points of segment. Minimal distance is distance from segment.
Computation distance from segment using these math formulas isn't too much smart. We use different way. We pre-computate inverse transformation matrix for each segment(edge), which "transfer" an segment to the origin of coordinates. Computation of distance from such segment is much more simple.
Ilustration of transformation in 2D:
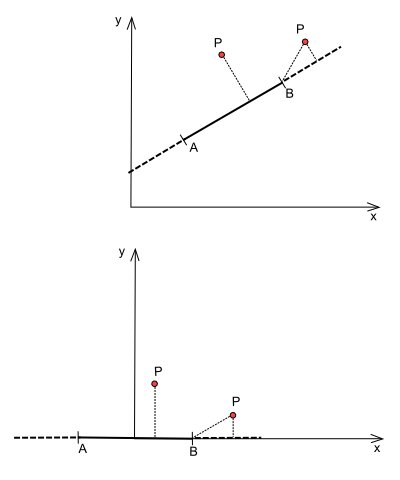
|
We don't have transform segment with inverse trnasform matrix, because we know, that transformed segment will lay in the origin of coordinates. We have to transform only point P=X[x,y,z,w] w (weight of point is 1):
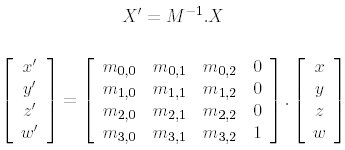
|
This transformation could be computate using modern instruction set (MMX/SSE) of our processors.
Computation of distance transformed point from segment laing in th origin of coordinates is very easy then:
/* simplificated densfunc() in mball.c
* vec ... coordinates of point X
* ball ... segment primitive */
float densfunc(MetaElem *ball, float *vec)
{
float dist2;
Mat4MulVecfl(ball->imat, vec);
if(ball->type==MB_EDGE) {
if( vec[0] > ml->expx) vec[0]-= ml->expx;
else if(vec[0]< -ml->expx) vec[0]+= mll->expx;
else vec[0]= 0.0;
}
/* only powers of distance squared are used in blending function */
dist2= (vec[0]*vec[0] + vec[1]*vec[1] + vec[2]*vec[2]);
/* calculation of blending function */
dist2= 1.0f-(dist2/ball->rad2);
if(dist2 < 0.0) return 0.5f;
return 0.5f-ball->s*dist2*dist2*dist2;
}
Triangle (Face)
I captured several demonstraiting videos of my devel version:
- http://e-learning.vslib.cz/~hnidek/captured-videos/meta-mesh.avi
- http://e-learning.vslib.cz/~hnidek/captured-videos/point-dist.avi
- http://e-learning.vslib.cz/~hnidek/captured-videos/meta-edge-ellipsoid.avi
Jiří Hnídek 01 Nov 2004