利用者:Jaredr122/Doc:2.6/Manual/Modeling/Curves

Curves

Curves and Surfaces are objects just as meshes are objects except they are expressed in terms of mathematical functions, rather than as a series of points.

Blender implements both Bézier curves and Non-Uniform Rational B-Splines (NURBS) curves and surfaces. Both are defined in terms of a set of “control vertices” (or “control points”) which define a “control polygon”, though each follow a different set of mathematical laws. The way the curve and the surface are interpolated might seem similar, at first glance, to Catmull-Clark subdivision surfaces. The curve is interpolated while the surface is attracted.

Compared to Polygonal Mesh

One main advantage to curves over polygonal meshes is that curves are defined by less data, so can produce excellent results using less memory and storage space at modeling time. However, this procedural approach to surfaces can increase demands at render time.

Some modeling techniques like extruding a profile along a path are only possible using curves. At the same time, vertex-level control is more difficult when using curves.

There are times when curves and surfaces are more advantageous than meshes, and times when meshes are more useful. It is recommended you read the section on mesh editing, which should help you decide whether to use meshes or curves in your project.

When you have finished reading and learning about Bézier and NURBS curves there are several more advanced examples on the application of curves in the tutorials section for modeling complex objects.

Logo Thumbnail.

There is a Working example that shows how to create an interesting bird-like logo. The tutorial covers most aspects of working with Bézier curves including: adding curves, setting up a background image as a template guide and beveling the final curve.

In addition, the Tutorial section has examples on both Skinning and Curve deform techniques.

Curve Primitives

Blender has five different curve primitives, two Bézier and three NURBS:

Bezier Curve

adds an open 2D Bézier curve with two control points.

Bezier Circle

adds a closed, circle-shaped 2D Bézier curve (made of four control points).

NURBS Curve

adds an open 2D NURBS curve, with four control points, with Uniform knots.

NURBS Circle

adds a closed, circle-shaped 2D NURBS curve (made of height control points).

Path

adds a NURBS open 3D curve made of five aligned control points, and with Endpoint knots and the CurvePath setting enabled.

Curve Structure

About U and V coordinates U and V are the conventional names of parametric “coordinates” components (note that these are the same names as texture ones…). They are used to define the resolution, the “knots” for NURBS, etc., along given “axis”. For curves, only the U component is relevant (as they have only one dimension, they are lines). The V component is used by NURBS surfaces.

Control Points and Segments

Curves are mainly defined by their control points, as described below in their respective section. However, you will sometimes encounter another concept, the “segment” of curve. A segment is defined implicitly by its two adjacent control-points. Unlike with meshes, you can’t explicitly select a segment – you must select its two adjacent control-points.

Normals

Bézier curve example.

NURBS curve example.

In Edit mode, the curve is drawn as a black line, and in Solid shading (or Shaded, …), the closed curves are filled with a flat surface. 3D curves have additional “arrows” all along the curve, illustrating both the direction and the relative speed of the movement objects will have when following them as path (unless a custom Speed Ipo is defined…).

Each control point is drawn in purple. Bézier “vectors” are materialized with pink lines, whereas NURBS vertices are linked by yellow lines. As with meshes, selected vertices are highlighted in yellow (with a lighter shade for the active element).

Shape

2D and 3D Curves

By default, new curves set to be 3D, meaning control points can be placed any where in space.

Curves can also be set to 2D, which constrains the control points to the curve object's local XY axis. 2D curves that are closed will render as filled regions (see below).

Curve Resolution

Although these curves are continuous mathematical objects, they must nevertheless be represented in discrete form (set of small segments) from a rendering point of view. This is done by setting a resolution property, which defines the number of points which are computed between every pair of control points. Note that this applies only to Bézier curves, and is different for NURBS.

You have in fact three resolution settings, two in the Curve and Surface panel, and one in the Curve Tools panel:

• DefResolU: The resolution applied by default to all curves of the object, both in the 3D views and at render time.
• RenResolU: The resolution applied by default to all curves of the object when rendering, if not set to zero (else DefResolU is used).
• Resol U: This setting is only available in Edit mode, it will modify the resolution of the curves (partly) selected currently. Note that it is reset to the DefResolU value each time you modify this setting.

Bézier resolution example.

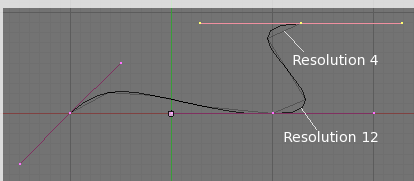
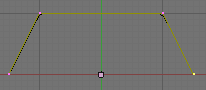
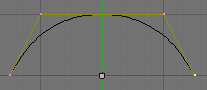
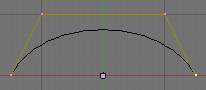
A separate resolution can be set for each curve by adjusting the DefResolU field of the Curve and Surface panel. The default is 6. (Bézier resolution example) is an example of the same curve, superimposed with the aid of Gimp, showing two different resolution settings. The lighter shaded curve has a low resolution of 4; the curve begins to look linear. The darker curve has a resolution of 12 and is very smooth. Note that high resolutions may look nicer but they can slow down interactive rendering if there is a large number of curves (and/or if these ones have a large amount of control points).

Fill

The way a curve can be filled depends on whether it is 2d or 3d, and if it has Beveling or Extrusion and if it is cyclic.

A 2d closed curve will be filled and render as a flat planar shape, unless bevel or extruded.

Twisting

The orientation of the curve normals is greatly affected by the shape of the curve. Several options allow you to further control how the normals are oriented.

Closed and Open Curves

Curves (Bézier or NURBS) are mono-dimensional: they are lines, that never crosses themselves (i.e. control points are only linked to at most two others, forming a continuous line, without any fork…). However, curves can be open (i.e. they start and end points are not linked by a curve segment) or closed. Closed curves are solid, inasmuch that Blender adds a solid flat face inside them (unless they are made 3D).

Spline Types

Nurbs and Bezier curves have different properties and controls that affect how they appear. These are primarily under the Active Spline section of the curve properties.

Béziers

Bézier curves are the most commonly used curves for designing letters or logos. They are also widely used in animation, both as paths for objects to move along and as F-curves to change the properties of objects as a function of time.

Curve example.

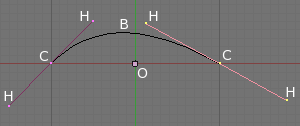
(Curve example) is the most basic Bézier curve you can create. It consists of two control points or vertices, labeled “C”, the curve “B”, handles “H” and an object center “O”.

A handle “H” defines the tangent vector to the curve in point “C” (on its side). The “steepness” of the curve is controlled by the handle’s length (“H” to a “C”). The longer a handle is the steeper the curve (i.e. the more curve wants to hug the handle).

There are four types of handles (Types of Handles for Bézier curves):

• Free Handle (black). The handles are independent of each other. To convert to Free handles use V,F
• Aligned Handle (purple). These handles always lie in a straight line, and give a continuous curve (without sharp angles…). Hotkey: V,L.
• Vector Handle (green). Both parts of a handle always point to the previous handle or the next handle (this allows you to create curves made of straight lines!). Hotkey: V,V.
• Automatic Handle (yellow). This handle has a completely automatic length and direction, set by Blender to ensure the smoothest result. Hotkey: V,A.

You can also use V,T to toggle between Free and Aligned.

Types of Handles for Bézier curves.

Handles can be grabbed, rotated and scaled exactly as ordinary vertices in a mesh would. As soon as the handles are moved, the handle type is modified automatically:

• Auto Handles becomes Aligned;
• Vector Handles becomes Free.

NURBS

NURBS curves are defined as rational polynomials and are more general, strictly speaking, than conventional B-Splines and Bézier curves inasmuch as they are able to exactly follow any contour. For example a Bézier circle is a polynomial approximation of a circle, and this approximation is noticeable, whereas a NURBS circle is exactly a circle. However, a NURBS cannot have real sharp angles in it, unlike a Bézier curve…

NURBS curves require a little bit more understanding of the underlying components that make up a NURBS curve in order to get full use of them. They have a large set of variables, which allow you to create mathematically pure forms. However, working with them requires a little more discussion on the various parts of a NURBS curve.

Note NURBS are a very complicated topic, I think they might be a good subject for a “Theory” article – written by someone knowing them deeply! (For a start, here's the Wikipedia page.)

Knots

We start with Knots. NURBS curves have a knot vector, a row of numbers that specifies the parametric definition of the curve (i.e. they describe the range of influence for each of the control-points). Remember the control-points from Bézier curves, NURBS have them too and each control-point affects some part of the curve along that range. The control-points appear as purple vertices.

Note that knots setting concerns only open NURBS, not closed ones.

Default Uniform curve.

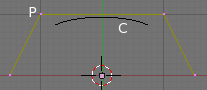
(Default Uniform curve) is the default NURBS curve created using the NURBS Curve menu item from the toolbox’s Add menu and is an example of a Uniform curve. The curve itself is drawn in black, labeled “C” and the control-points are drawn in purple; one out of the 4 is labeled “P”.

You can’t manipulate the Knot vector directly but you can configure it using three presets: Uniform, Endpoint and Bezier.

The Uniform button of the Curve Tools panel produces a uniform division for closed curves, but when used with open curves you will get “free” ends, which are difficult to locate precisely.

Endpoint curve.

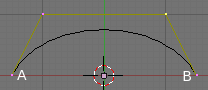
The Endpoint button sets the Knot vector in such a way that the first and last vertices are always part of the curve, which makes them much easier to place. (Endpoint curve) is an example of applying the Endpoint button to the (Default Uniform curve). You can see that the curve has now been pulled to the end control-points labeled “A” and “B”.

Bezier NURBS, Order 3.

Bezier NURBS, Order 4.

Finally, Bezier “Knot vector” (I’m not really sure this remains a real knot, in fact…) make the NURBS control points mimic the Bézier control points behavior. This works only with two orders value (see below): 3 and 4.

• With an Order of 3, all odd points act as a center of a Bézier control point, and all even points act as a Bézier handle. So vertices (1,2,3) define a first Bézier segment, (3,4,5) a second one, and so on…
• With an Order of 4, all four groups of control points define a Bézier segment, i.e. vertices (2,3,4,5) define a first segment, (5,6,7,8) a second one, etc. Note that here, the first vertice is for some reasons unused…

Order

The Order field of the Curve Tools panel is the “depth” or degree of the curve (i.e. you are specifying how much the control-points are taken into account for calculating the curve shape).

Order 1 is a point and is not an available depth setting, Order 2 is linear (Order 2 curve), Order 3 is quadratic (Order 3 curve), (Order 4 curve) is cubic, and so on. The valid range is 2 to 6. Notice that as the Order rises the curve moves away from the control-points.

Order 2 curve.

Order 3 curve.

Order 4 curve.

If your curve has 6 or more control-points the Order can not be set higher than 6. 6 is the highest Order allowable. If you have less than 6 control-points then the highest Order is limited by the number of control-points. For example, if your curve has 5 control-points then the highest Order allowable is 5.

Always use an order of 5, if possible, for curve paths because it behaves fluidly under all circumstances, without producing irritating discontinuities in the movement. For example, if you have a cube assigned to travel along a NURBS path with an Order of say 2 then the cube will appear to move roughly (or jerky) along the path.

Math Note Mathematically speaking the Order is the order of both the Numerator and the Denominator of the rational polynomial defining the NURBS curve.

Poly Curves

Poly Curves are essentially Nurbs curves of degree 2, or a bezier curve set to vector handles. The segments between points are always linear.