「利用者:Mont29/Foundation/Split Vertex Normals」の版間の差分
(→Handling normals in mesh modifications) |
細 (1版 をインポートしました) |
(相違点なし)
| |
2018年6月29日 (金) 06:04時点における最新版
目次
Split Vertex Normals
Disclaimer: WIP!
I will work in a local branch and use & update D11 on a regular basis.
Current situation
Right now, we have only one normal per vertex, stored as a char[3] in the vertex data itself.
In addition, we can compute ondemand split normals as a CDLoop layer (i.e. one normal per vertex and per polygon), but for now it is not persistent, and only used to export sharp edges in OBJ/FBX formats.
What to Add - Overview
I see at least those goals:
- Preview per-loop normals - DONE 2.71.
- Tangent data - DONE 2.70.
- Loop normal edition - this is the most complex part, I would subdivide it the following topics:
- Handling normals in mesh modifications - i.e. data model!
- Generating normals.
- Importing & editing normals.
Details
Preview per-loop normals - DONE 2.71
This should not be too much complex. Simply add a per-mesh option to use loop normals in 3D view, either using an existing loop CD_NORMAL, or computing it on final dm if needed (based on sharp edges and optional angle threshold, using existing code).
Render Engines
If we add that support to renderers as well, we could simply reuse settings in the Mesh prop’s Normals panel, to get a coherent and consistent behavior in both 3D view and renders, right now this is a bit confusing…). That’s more like a side topic though, I don’t know how much work it would be to add support of loop normals to BI and Cycles, and won’t take time to investigate this for now.
|
In current patch, we have the code to compute final DM loop normals, convert them to tessface data, and use them in OpenGL 3DView drawing, as well as BI.
Tangent data - DONE 2.70
Compute/export of the tangent space data as well (tangent vector, and ±1.0 float value to give direction of remaining bitangent vector) - already have a patch for this, using mikktspace and a similar approach as current loop normals computation. Note tangent space is only meaningful with tris/quads, so current patch just abort calculations when ngons are present in the mesh.
Manual Edition of tangent space?
Todo: ask users whether custom tangent space could be useful… If not (I hope so!), current implementation should be final one.
|
Loop normal edition
Now that is the big piece.
Loop normals should obviously be optional, with ways to add and remove them from a mesh (similar to e.g. to the Skin modifier’s data).
Handling normals in mesh modifications
Here is a detailed description of solution chosen for now - a loop normal space, common to all loops of a same “smooth fan” (at the end of this section I kept early reflexions/ideas).
First, some definitions:
- Smooth/Sharp vertex
- A smooth vertex is exclusively used by smooth edges.
- Smooth/Sharp edge
- A sharp edge is either tagged as such, non-manifold (i.e. used by more or less than exactly two faces), and/or manifold but used by two faces having opposed normals (i.e. opposed winding).
- Smooth fan
- A set of loops sharing the same vertex, and belonging to faces joined by smooth edges only. Unless the related vertex is smooth, the start and end edges of the fan are sharp ones (they may be the same).
Each smooth fan has only one automatically-computed loop normal, one custom loop normal, and one loop normal space. In other word, they always have a single loop normal, even if it’s a customized one - you have to use a new sharp edge to split the smooth fan in two if you want to get two different custom loop normals.
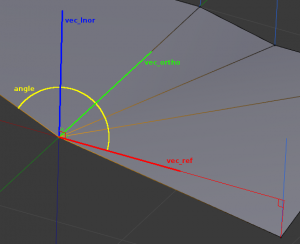
Now, the loop normal space.
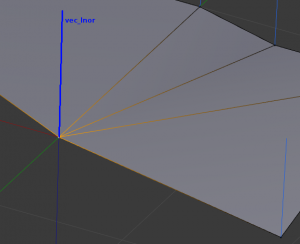
Our first axis is the auto-computed loop normal itself! This is the most important one, our main “reference” for custom normals.
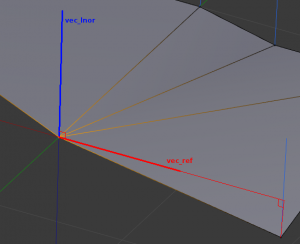
This axis is the normalized projection of the first edge of the loop onto the “lnor plane” (i.e. the plane orthogonal to the loop normal).
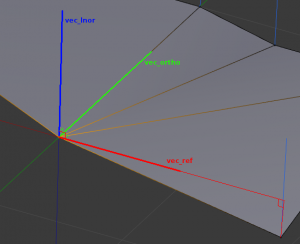
We also store a third axis, orthogonal to both vec_lnor and vec_ref. This axis is not needed to define our loop normal space, we only compute it because we need it in conversions (more about this later).
The third element that defines our loop normal space is the angle between vec_ref and the projection on the lnor plane of the other end edge of the smooth fan (in a ]0.0, 2pi] range, we keep the null value to tag invalid loop normal spaces).
This space has the advantage to “follow” the deformations of its smooth fan of loops. The only case a bit hard to manage is smooth vertex (i.e. a smooth fan cycling completely around a vertex, without any obvious start or end) - current implementation simply choose the edge related to the first loop entering this fan as reference in this case, it’s too weak to survive correctly to topology changes, but we can’t do much about it imho.
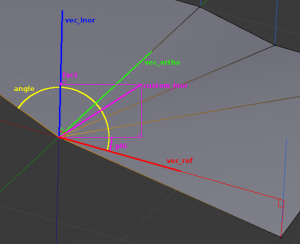
In this space, custom loop normals are represented by two rotations, but encoded differently.
The first one (fac1) is the dot product of the custom_lnor against the vec_lnor (i.e. the cosine of the angle between those two vectors). This means this angle is “absolute”. This changed, since it did not handled well the 'cone case' (move tip of cone vertically, you have to get custom normals there to adapt to the changes in angle between autlnors and edges). So now, it’s an angle factor too, 0.0 meaning aligned with autolnor, 1.0 is average angle between edges and autolnor (and yes, I know, picture is no more up to date :/ ).
The second one is a factor of a “phi” rotation around vec_lnor, such that:
- A 0.0 value means the custom_lnor is in the (vec_lnor, vec_ref) plane.
- A value between 0.0 and 1.0 means the rotation is “inside” the smooth fan (i.e. a portion of our “angle” lnor space value).
- A value between 0.0 and -1.0 means the rotation is “outside” the smooth fan.
In other words, this rotation is kept relative to the “fan angle” (projected in the lnor plane).
This way of representing custom loop normals remains consistent in pretty much all deformation cases (simple transformations, shears, fan growing/shrinking, etc.), it should only break in extreme/degenerated situations (like if one or both of the end edges being aligned with the auto loop normal), in which case we simply fall back to using auto lnor. It should also remains relatively consistent in some topology-change cases, but not in all of course!
(end of “modern” version, old ideas now)
The main issue is to decide what we do with custom normals when we modify somehow the mesh (modifiers, Edit mode…). This intimately related to the data model we chose. After talking with Campbell, I see the following possibilities currently:
- I - Store custom normals literally.
- We would just use/manipulate loop normal as other normals…
- pros: The simplest solution!
- cons: Needs to add a flag to loops, to distinguish those “custom edited” from “default” ones.
- cons: When deforming the geometry, we could recompute “default” normals, but “custom” ones would remain as-is, which would not give good results.
- II - Store custom normals as a diff vec in some kind of “local loop space”.
- In other words, store the custom normals relatively to the face's normal, in a kind of tangent space.
- pros: Allows to keep “valid” custom normals while deforming the geometry.
- cons: Complexity - Well, it’s not that complex, but still, it’s some kind of tangent space that have to work even for complex polys - I guess using e.g. face's normal as Z, loop vector as X (and Y as their crossproduct of course).
- cons: Needs to add a flag to loops, to distinguish those “custom edited” from “default” ones.
- cons: Loss of smoothing - When two adjacent loops (same vert) from adjacent faces share the same normal, that point is smooth between those two faces. There may be workarounds, but they would unlikely be simple nor time-light!
- III - Store custom normals as a diff vec from default (reference) normals.
- pros: Allows to keep “valid” custom normals while deforming the geometry (though probably less precisely than with II in full custom normals cases).
- pros: More easy than II to setup and use in general (on dev POV, no exotic per-loop space to compute, everything happens in good old object space…).
- pros: Easily solves the “smooth” problem, smooth vert will have the same ref normal for all related loops, so if the diff normals are the same as well, smoothing is preserved.
- pros: Easily marks which normals are "custom edited", and which ones are "default" (their diff are a null vector!).
- pros: I think it should also behaves quite well in additive/destructive editing scenario. Hard to think to everything here, though.
- cons: The need to have two vectors per loop (ref normal and diff vec), but we may be able to avoid this, by only computing ref vectors temporarily when needed (on import, in Edit mode, in final DM, etc.), and storing only diff vectors. So mem overhead would only really be sensible (i.e. durable) in Edit mode, not sure it could be a real problem in this case?
- IV - Mix II and III.
- Use diff to default loop normal in object space for loops sharing normals with adjacent ones (smooth loops), and diff in own face's tangent space for "sharp" loops (i.e. loops which both edges are marked as sharp).
- pros: Allows to keep “valid” custom normals while deforming the geometry.
- pros: Easily solves the “smooth” problem, smooth vert will have the same ref normal for all related loops, so if the diff normals are the same as well, smoothing is preserved.
- pros: Easily marks which normals are "custom edited", and which ones are "default" (their diff are a null vector!).
- pros: I think it should also behaves quite well in additive/destructive editing scenario. Hard to think to everything here, though.
- cons: The need to have two vectors per loop (ref normal and diff vec), but we may be able to avoid this, by only computing ref vectors temporarily when needed (on import, in Edit mode, in final DM, etc.), and storing only diff vectors. So mem overhead would only really be sensible (i.e. durable) in Edit mode, not sure it could be a real problem in this case?
- cons: Complexity - (same remarks as for II).
Currently solution III has my preference as a first step. I think it should be relatively easy to implement, and give good results in most cases. Further more, it should be possible to code it in a way that implementing IV later would not need much changes outside of loop normal code.
Generating normals
This is the process of overriding all or a selection of normals using some “procedural” algorithm.
- The default normals generation, based on geometry (face normals, boundaries, etc.) and sharp edges.
- The "Tree-process" which assigns to each loop the normal of the nearest point of the surface of another object, used in games to give trees, grass, etc., based on a few planes a more natural lighting.
- Others?
That kind of tools can be either operators and/or modifiers.
Importing & editing normals
A smart importing of loop normals should be able to detect sharp edges from normals values, and then “default” normals (matching default ones generated by Blender) from “custom” ones (note that if we use the III data layout proposed above, that later part is trivial). We should probably provide an API callback to compute sharp edges from a given set of loop normals, this should not be that complicated…
As for manual editing, we can keep it reasonably simple in a first time, and then expand it into a full-featured version (with a loop-normal select mode, etc.).
One key point would be to be able to edit loop normals in “smooth groups”, with tools to separate/merge them (actually affecting smooth edges flags). And obviously, visualization (preview per-loop normals together with a new show_loop_normals in “Mesh Display” panel).
“Simple edition” would be something like a new panel in 3D view properties, active only when a single vertex is selected, with a vector property for each loopgroup…
“Fullfeatured” edition would add a new “type” to vert/edge/face, with its own select mode, and set of tools.
I would stick to the simple version for now, being careful that design makes it possible to extend it later.