利用者:Mats Halldin/Sandbox/Incubator-003

Introduction to topology.

Euler's theorem

Euler's theorem

Let P be a polyhedron which satisfies:

(a) Any two vertices of P can be connected by a chain of edges (i.e. there are no faces missing and no "Non-Manifolds".)

(b) Any loop on P which is made up of straight line segments separates P into two pieces (i.e. a mesh without holes like in a donut.)

Then <math>v-e+f=2</math> for P.

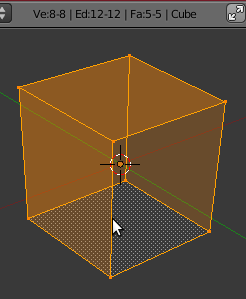
Default cube

Default cube selected in edit mode

If we add a cube and tab into edit mode, all vertices are select by default and above the 3D view Blender is informing us that

Ve:8-8 | Ed:12-12 | Fa:6-6 | Cube

which, of course, means we have selected all eight vertices, twelve edges, and six faces of our object Cube.

According to Euler's theorem

<math>v-e+f=2</math>

if we take the number of vertices (v), subtract the number of edges (e), and add the number of faces (f)

<math>8-12+6</math>

we get 2.

A face extruded

Triangulated

If we extrude a face from our cube, Euler still returns

<math>12-20+10=2</math>.

And if we hit CtrlT to transform all quads into tris, Euler still returns

<math>12-30+20=2</math>.

Face deleted

On the other hand, if we remove a single face from our original cube, Euler returns

<math>8-12+5=1</math>

instead.

Other simple primitives

Let's test Euler's theorem on other well-known geometric primitives:

Now, add a default UV Sphere and tab into edit mode. Blender now informs us that

Ve:482-482 | Ed:992-992 | Fa:512-512 | Sphere

and Euler returns

<math>482-992+512=2</math>.

Extruding (<math>486-1000+516=2</math>) or deleting (<math>482-992+511=1</math>) a face from the UV sphere is not changing the output from Euler's formula.

Same goes for the default cylinder

Ve:576-576 | Ed:1152-1152 | Fa:576-576 | Cylinder

<math>66-160+96=2</math>.

We might first hope that this is a golden rule that applies unconditionally to all meshes.

Some more complex cases

The default torus

Ve:576-576 | Ed:1152-1152 | Fa:576-576 | Torus

<math>576-1152+576=0</math>.

A monkey

Cubes, spheres, and even toruses are well-known geometrical shapes, but what about Suzanne, our monkey? In edit mode, Blender tell us

Ve:507-507 | Ed:1005-1005 | Fa:500-500 | Monkey

and Euler returns

<math>507-1005+500=2</math>.

Looks familiar. However, if we deselect everything and Ctrl⇧ Shift⇆ TabM to select Non-Manifolds, Blender selects two pairs of loops, namely the holes for the eyes. Apparently, the monkey is topologically distinct from the default cube.

Furthermore, if we CtrlT on the monkey and select all tris, we get

<math>507-1472+968=3</math>.

Selecting non-manifolds again returns an additional edge near the nose.

Uh-huh, topology-wise something is wrong here.

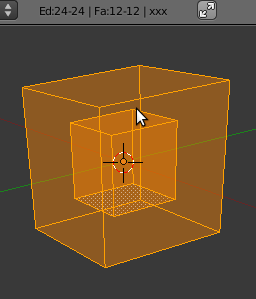
Cube with interior cube

Interior cube

Select all vertices of the default cube, ⇧ ShiftD to duplicate, and S to scale it down. Our mesh now has two cube, one inside the other. Blender tells us

Ve:16-16 | Ed:24-24 | Fa:12-12 | Cube

and Euler returns

<math>16-24+12=4</math>.

This is new...

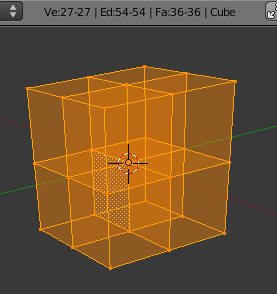
Cube with interior faces

Interior faces

<math>27-54+36=9</math>

Möbius strip and Klein bottle

A Möbius strip

<math>32-48+16=0</math>

A Klein bottle is what you get if you glue two Möbius strips together along a common edge.

<math>624-1248+624=0</math>

Odd as they come, these two meshes are, according to Euler's theorem, similar to a circle...

Conclusions

Is there any logic to this?

• Circle=0
• Disc=1
• Cylinder=2

• If two polygons meet they do so in a common edge, and each edge of a polygon lies in precisely one other polygon.
• At any vertex, faces fit together to form a piece of surface around that vertex.
• Is there a loop that does not separate the mesh into two distinct parts?

References

• Armstrong, M. A. (1983), Basic Topology, Springer, pp 1–12, ISBN 0387-90839-0.