Dev:Source/Data System/Dependency Graph/Implementation

-- JLucPeuriere - 28 Nov 2004

Description

Current blender code doesn't handle cleanly and accurately the refresh to all changes to objects implied by parenting and deformers. Current method is also slow with armatures as everything is calculated twice. This project aim to create a dependency graph to both evaluate things in the correct order, and update only those which need to.

Note This is not a scene graph which is another model.

Note 2 Dependency graphs could be used too for node based materials, but this would need rewrites in render code, and isn't the current goal.

Directed Acyclic Graph

The correct way of handling such dependencies is a directed acyclic graph (DAG). This is a very common and well studied structure in graph theory which can be applied to the task. It can be viewed as an extension of the tree structure where branches are allowed to merge. DAGs are very often used for scheduling applications.

http://www.cs.mcgill.ca/~cs251/OldCourses/1997/topic25/

http://www.ics.uci.edu/~eppstein/161/960208.html

Once the DAG is built, it can be queried to show which object depends on another, and also find an order of evaluation respecting all dependencies as long as there are no cycles in them. As a secondary task, it can be used to check a new relation won't induce cycles. We will see that those simple tasks provide quite versatile services. If a cycle is created by a new relation, we need to create rules for breaking this cycle. The relations forming a cycle (strongly connected components) can be considered as a single node in the DAG for evaluation order of other relations.

Dependencies in blender - relations types

object/objects class relations

fig 1

fig 2

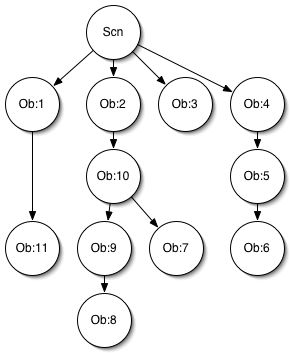
• objects basic parenting : simplest one, depends on position & rotation, affect position and rotation. Is a tree so no cycle can occur there.

fig 1 shows a typical tree. Arrows show the parenting relations. As an object can have only a single parent, we can define easily an order for calculating the transformations.

We have attached all root objects to the scene in order to have a single graph, and not many separate ones.

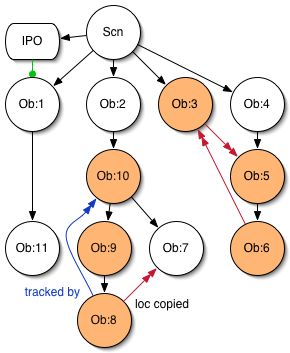
• world object IPOS : loc, rot, and size affect corresponding value of a single objet, direct dependency
• object constraints : copy, track, stretch depends on position & rotation, affect position size and rotation. Influence should be also considered as a priority imho.

fig 2 shows IPOS and constraints attached. Note that relations are inverse of constraints, to show which depends on which. We have 2 cycles here, 8-9-10 & 3-5-6. 7 is not part of a cycle. the DAG cannot handle this and deliver a valid order, so cycles must be broken outside of it.

Those dependencies affect objects as a whole and so are independent of the deformers below.
On those, only constraints can create a cycle. Object constraints can also link to armature bones. In this case, the whole bone system must be promoted at object level?

fig 3

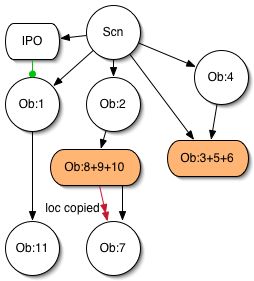
As stated previously and as shown in fig 3, a valid DAG can be returned if we consider each cycle as a single node. It is then up to the caller to break the cycle.

Time IPOs can also offset other IPO positions in each object and so are ancestors of any same object IPO.
Is path a first level constraint ? (I think so).

Duplis can't be calculated before deformers.

• to break cycle dependencies at this level for constraints,
• we can first break around the six degrees of liberties. it should be enough very often.
• then use influence as priority factor by cutting the lowest values from the DAG, and calculate them later
• solve an equation system (hopefully it will be linear ?)
• iterate the system in a solver (eg IK ?)

Once relations of this class are calculated, we can continue on other relations, after having done the transformations in the topological sort order of the DAG. We are sure this order is correct and won't change. The only exception is vertex children that we can't calculate yet. The sub-DAG of all the object is calculated once.

object/vertex class with object being a control object

• *armatures bones*
• *lattices and curves deformers* vertex (global poses are at level 1)
• keyframes
• actions
• ikas
• constraints
• *metaballs components*

Same calculations as in previous level. Those relations are most likely independent subgraphs. However we can have strongly dependent components and/or mutual constraints, so this step can be repeated more than one time. The goal here is to get a correct transform, without the lags that affect complex armatures in blender. By the way, that means that old armatures can behave differently once we switch to new code, so we must ask ourselves if we do the switch or give the new system alongside. My preference goes to the latter for compatibility reasons.

object/vertex class

• all deformers stack (order of deformations can vary or be chosen by artist ?, should be evaluated only if a parent has changed as they can be costly)
• vertex keys
• hooks
• subsurfs
• lattices
• curves
• effects
• particles (?)
• all objects in same layer (all objects are parents of particle vertex)
• particles can be also considered as control object of their own vertices and go upper
• sofbodies
• collisions (ditto)
• sofbodies can be also considered as control object of their own vertices and go upper
• duplis objects
• polygonized metaball

only applying stacks

---+++vertex/object class

• vertex parenting

This class is a bit special, as to solve it, we need either to promote the mesh at object level (not very smart imo) or to cut the DAG in 2 evaluated in order, the 2nd DAG including all parents and children of the parented object siblings

DAG construction

We can either rebuild the DAG each time we need it (less efficient but also less intrusive to blender code), or dynamically by updating it at each change. The 2nd solution gives us more liberties and insures things are evaluated in the same order in subsequent frames (can be useful if we had to break a cycle).

As a first step it's easier to rebuild each time, DAG code itself is simple (we dont neeed insane optimisations, the number of relations is reasonable), the real meat is in correctly taking all informations from scene-base.

We will use an adjacency list structure (see upper) which can store both a DAG and a cyclic graph.

The DAG is used to get only an order of evaluations so it should be as independent as possible and not act directly on objects.

Evaluating and using the DAG

We want to :

• add and remove nodes and relations
• test for acyclicity
• get strongly connected nodes sets to solve, then reinput to get finally a DAG usable for sorting
• get a topological sort for a complete refresh
• get all childs from a given node (getting parents is easy too), eg for a limited refresh
• get a sub-tree for recalculating transforms

objects groups api ?

Python access to objects vars can do some mess in that too, and must be taken in account.

As discussed with Ton, a nice thing to do is to use the oops window to optionally show the DAG and relationships.
It will be also useful when coding system.

Ton thinks that we can merge the vertex and objects nodes as single. Must be checked.

Data structures

enum {
    DAG_WHITE = 0,
    DAG_GRAY = 1,
    DAG_BLACK = 2
};

typedef enum { //more to come
    DAG_RL_SCENE,
    DAG_RL_DATA,
    DAG_RL_PARENT,
    DAG_RL_TRACK,
    DAG_RL_PATH,
    DAG_RL_CONSTRAINT
} dag_rel_type;

typedef struct DagAdjList
{
    struct DagNode *node;
    dag_rel_type type;
    int count; // number of identical arcs
    struct DagAdjList *next;
} DagAdjList;


typedef struct DagNode
{
    int color;
    short type;
    float x, y, k;	
    void * ob;
    int BFS_dist;		// BFS distance
    int DFS_dist;		// DFS distance
    int DFS_dvtm;		// DFS discovery time
    int DFS_fntm;		// DFS Finishing time
    struct DagAdjList *child;
    struct DagNode *next;
} DagNode;

typedef struct DagNodeQueueElem {
    struct DagNode *node;
    struct DagNodeQueueElem *next;
} DagNodeQueueElem;

// queue use recycling of freed nodes to avoid malloc/dealloc
typedef struct DagNodeQueue
{
    DagNodeQueueElem *first;
    DagNodeQueueElem *last;
    int count;
    int maxlevel;
    struct DagNodeQueue *freenodes;
} DagNodeQueue;

// forest as we may have more than one DAG unnconected
typedef struct DagForest 
{
    ListBase DagNode;
    int numNodes;
} DagForest;

Public API

struct Scene;
struct DagNodeQueue;
struct DagForest;

typedef enum { 
    DAG_RL_SCENE = 1,
    DAG_RL_DATA,
    DAG_RL_PARENT,
    DAG_RL_TRACK,
    DAG_RL_PATH,
    DAG_RL_CONSTRAINT,
    DAG_RL_HOOK,
    DAG_RL_DATA_CONSTRAINT,
    DAG_NO_RELATION
} dag_rel_type;


typedef enum {
    DAG_RL_SCENE_MASK,	  
    DAG_RL_DATA_MASK,								
    DAG_RL_PARENT_MASK,	
    DAG_RL_TRACK_MASK,	
    DAG_RL_PATH_MASK,  
    DAG_RL_CONSTRAINT_MASK,
    DAG_RL_HOOK_MASK,	
    DAG_RL_ALL_BUT_DATA_MASK,
    DAG_RL_DATA_CONSTRAINT_MASK,	
    DAG_RL_ALL_MASK				
} dag_rel_type_mask;

// queues are returned by all BFS & DFS queries
// opaque type
void *pop_ob_queue(struct DagNodeQueue *queue);  
int queue_count(struct DagNodeQueue *queue);  
void queue_delete(DagNodeQueue *queue);

// queries
struct DagForest *build_dag(struct Scene *sce, short mask); 
void free_forest(struct DagForest *Dag);
int pre_and_post_BFS(); // BFS with user defined functions when node is discovered
                        // and finished. not finished
int pre_and_post_DFS(); // ditto for BFS
struct DagNodeQueue *get_ancestors(struct DagForest *dag, void *ob); 
struct DagNodeQueue *get_childs(struct DagForest *dag, void *ob); 
dag_rel_type are_obs_related(struct DagForest *dag, void *ob1, void *ob2);
bool is_acyclic(struct DagForest *dag); 
int get_cycles(struct DagForest *dag, struct DagNodeQueue **queues, int *count); 
void topo_sort_baselist(struct Scene *sce);

-- JLP#9/03/05